理系数学の良問プラチカ　問題解説５　（東北学院大）

問題

\(a\)を定数とし、２次不等式\((x-a^2)(x+a-2)\)・・・①を考える。

• 1) ①を満たす\(x\)がただ１つ存在するように\(a\)の値を定めよ
• 2) ①の解\(1≦x≦3\)となるように\(a\)の値を定めよ
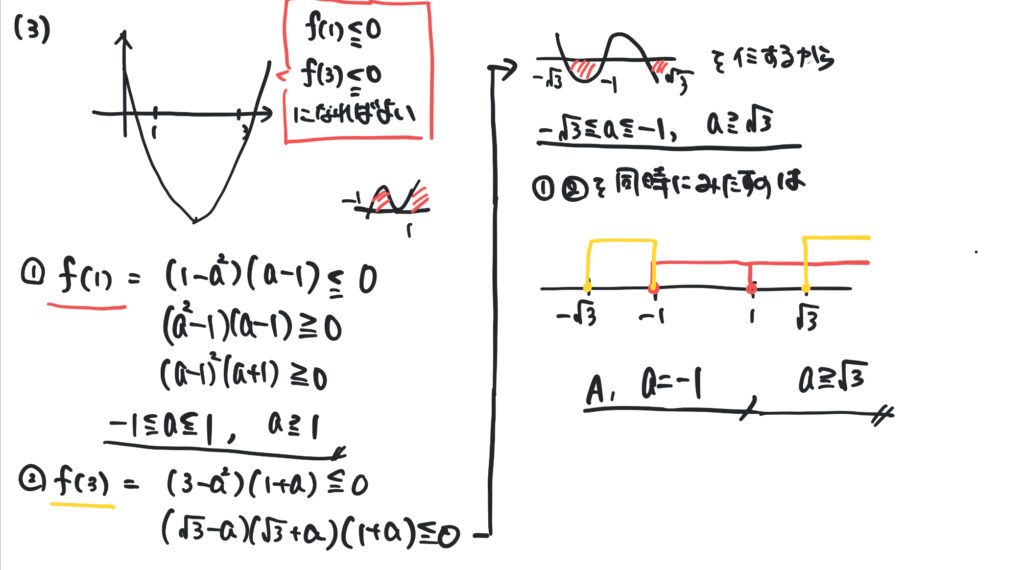
• 3) \(1≦x≦3\)ならば常に①が成り立つような\(a\)の値の範囲を求めよ

この問題を解くのに必要な前提知識

• ２次不等式の基礎
• ３次方程式のグラフ
• 組立除法など３次方程式の解の求め方

問題解説

感想と気づいたこと

2)の問題の捉え方が難しい。\(1≦x≦3\)の範囲に解が存在する条件かと思った。3)では、３次方程式のグラフや３次方程式で重解が発生したときのグラフがわからないとうまくグラフが書けない