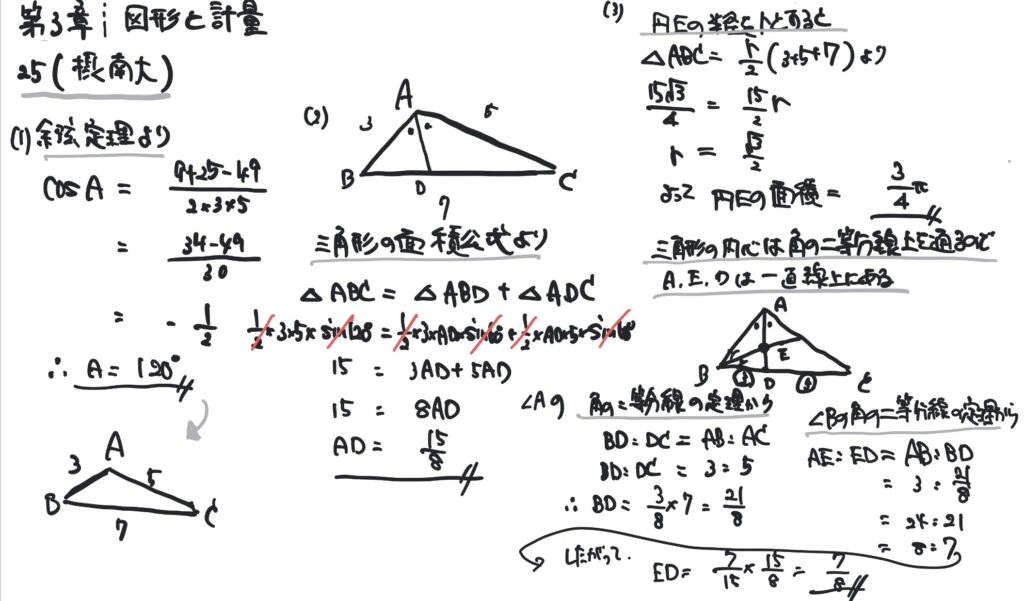
問題
三角形ABCの3辺の長さを
AB=3, BC=7, CA=5
とする。∠A, ∠B, ∠Cの大きさをそれぞれA,B,Cで表すとき
(1) Aの値を求めよ
(2) ∠Aの二等分線が線分BCと交わる点をDとするとき、線分ADの長さを求めよ
(3) 三角形ABCの内接円の中心をEとするとき、内接円の面積および線分EDの長さを求めよ
この問題を解くのに必要な前提知識
- 余弦定理
- 三角比の面積公式
- 内心の特徴
- 角の二等分線の定理
問題解説
感想と気づいたこと
- 基本的に、余弦定理→正弦定理と使うが、三角比の面積公式を使って長さを求めることもできる
- 角の二等分線2本の交点が内心
- 角の二等分線の定理をアングルを変えて2回使うこともできる



コメント