問題
\(x\)についての2次不等式\(x^2-(a+1)+a<0, 3x^2+2x-1>0\)を同時に満たす整数\(x\)がちょうど3つ存在するように定数\(a\)の値の範囲を求めよ
この問題を解くのに必要な前提知識
- 2次不等式
- 因数分解
問題解説
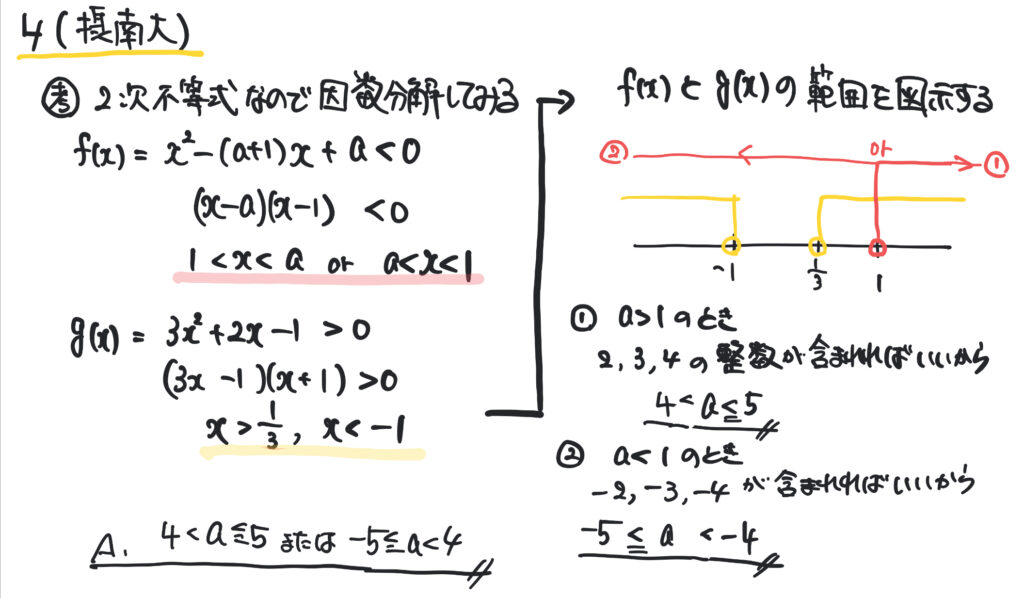
感想と気づいたこと
最初、平方完成などしてみたが、結局グラフの位置関係はよくわからなかった。因数分解して\(x\)軸との共有点を単純に探せばよかった。また、\(a=5\)になってもいいので不等式のイコールをつける場所に注意する。
 問題解説
問題解説\(x\)についての2次不等式\(x^2-(a+1)+a<0, 3x^2+2x-1>0\)を同時に満たす整数\(x\)がちょうど3つ存在するように定数\(a\)の値の範囲を求めよ

最初、平方完成などしてみたが、結局グラフの位置関係はよくわからなかった。因数分解して\(x\)軸との共有点を単純に探せばよかった。また、\(a=5\)になってもいいので不等式のイコールをつける場所に注意する。
コメント