問題
次の問いに答えよ
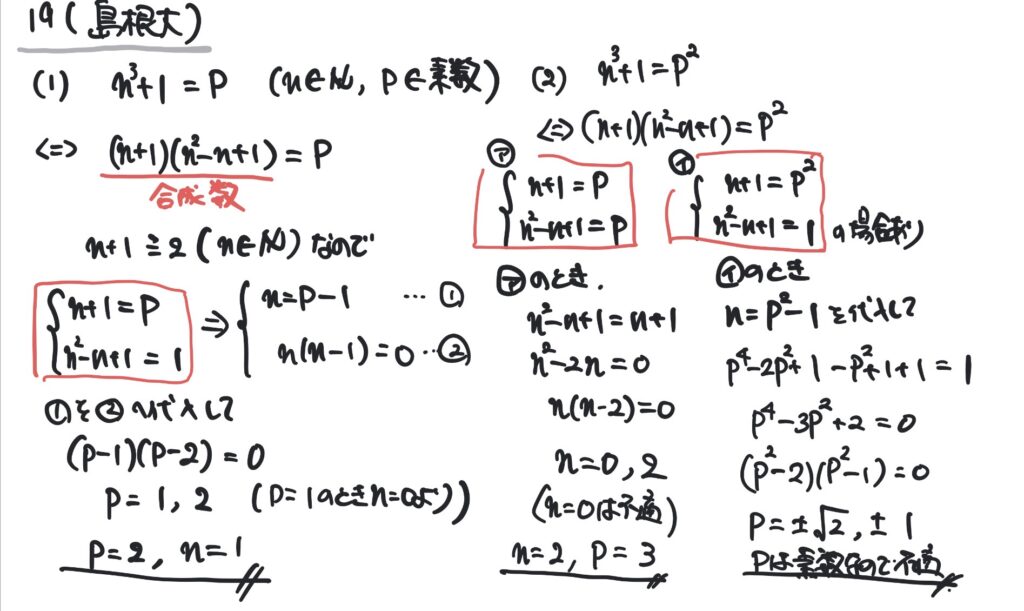
(1) \(n^3+1=p\)を満たす自然数\(n\)と素数\(p\)の組をすべて求めよ
(2) \(n^3+1=p^2\)を満たす自然数\(n\)と素数\(p\)の組をすべて求めよ
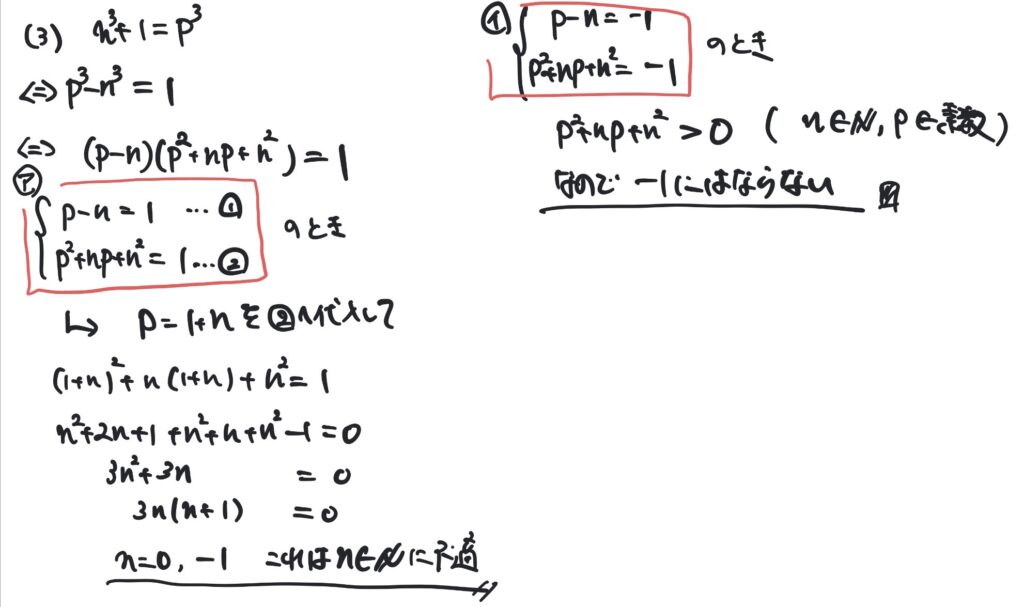
(3) \(n^3+1=p^3\)を満たす自然数\(n\)と素数\(p\)の組は存在しないことを証明せよ
この問題を解くのに必要な前提知識
- 3乗の式の因数分解
- 素数と合成数
問題解説
感想と気づいたこと
- \(p\)は素数なので、合成数で表すと\(1×p\)となりどちらかが1どちらかが\(p\)となる。」
- 3乗の場合は、\(=1\)にすると絞られる



コメント